Practica 2 - Autómata Celular

Practica #2 

Objetivos:

Programar un sistema adaptativo relacionado con cómputo evolutivo o sistemas 

complejos.(automata celular)

Elaborar un reporte donde describas tu trabajo y los resultados a los que llegaste

Introducción

Un autómata celular (A.C.) es un modelo matemático para un sistema dinámico que evoluciona en pasos discretos. Es adecuado para modelar sistemas naturales que puedan ser descritos como una colección masiva de objetos simples que interactúen localmente unos con otros. Son sistemas descubiertos dentro del campo de la física computacional por John von Neumann en la década de 1950. La teoría de los autómatas celulares se inicia con su precursor John von Neumann a finales de los década de 1940 con su libro Theory of Self-reproducing Automata (editado y completado por A. W. Burks).

Justificación

Seleccionamos el problema de los automatas ya que son patrones que, a pesar de estar basados en teorias, se encuentran en la naturaleza, lo cual no da mucha curiosidad y queremos representarlo graficamente en un programa de computo y poder experimentar con el.

Desarrollo

Para la Practica #2 seleccionamos el modelo de los Autómatas celulares donde crearemos en base a las reglas existentes para estos, un programa que, en base al algoritmo de los automatas, genere los 256 patrones.

Se puede describir a un A.C. como una tupla, es decir, un conjunto ordenado de objetos caracterizado por los siguientes componentes:

• Una rejilla o cuadriculado (lattice) de enteros (conjunto ) infinitamente extendida, y con dimensión . Cada celda de la cuadrícula se conoce como célula.
• Cada célula puede tomar un valor en  a partir de un conjunto finito de estados .
• Cada célula, además, se caracteriza por su vecindad, un conjunto finito de células en las cercanías de la misma.
• De acuerdo con esto, se aplica a todas las células de la cuadrícula una función de transición ( 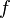 ) que toma como argumentos los valores de la célula en cuestión y los valores de sus vecinos, y regresa el nuevo valor que la célula tendrá en la siguiente etapa de tiempo. Esta función  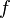se aplica, como ya se dijo, de forma homogénea a todas las células, por cada paso discreto de tiempo.

Por definición, un A.C. consiste de una retícula infinita de enteros. Sin embargo, para cuestiones prácticas (como en modelos de sistemas físicos llevados a cabo en ordenadores de memoria finita), se requiere tomar ciertas consideraciones a la hora de implementar un A.C. Por ello, la definición original se modifica para dar cabida a retículas finitas en las que las células del A.C. interactúen. Esto conlleva la consideración extra de lo que debe de suceder con aquellas células que se encuentren en los bordes de la retícula. A la implementación de una o varias consideraciones específicas se le conoce como condición de frontera.

Dentro del ámbito de los A.C., se pueden implementar numerosas condiciones de frontera, en función de lo que el problema real requiera para su modelado. Por ejemplo:

• Frontera abierta. Se considera que fuera de la lattice residen células, todas con un valor fijo. En el caso particular del juego de la vida y de otros A.C. con dos estados en su conjunto , una frontera se dice fría si las células fuera de la frontera se consideran muertas, y caliente si se consideran vivas.
• Frontera periódica. Se considera a la lattice como si sus extremos se tocaran. En una lattice de dimensión 1, esto puede visualizarse en dos dimensiones como una circunferencia. En dimensión 2, la lattice podría visualizarse en tres dimensiones como un toroide.
• Frontera reflectora. Se considera que las células fuera de la lattice "reflejan" los valores de aquellas dentro de la lattice. Así, una célula que estuviera junto al borde de lalattice (fuera de ella) tomaría como valor el de la célula que esté junto al borde de la lattice, dentro de ella.
• Sin frontera. Haciendo uso de implementaciones que hagan crecer dinámicamente el uso de memoria de la lattice implementada, se puede asumir que cada vez que las células deben interactuar con células fuera de la lattice, esta se hace más grande para dar cabida a estas interacciones. Obviamente, existe un límite (impuesto por la memoria disponible) para esta condición. Es muy importante no confundir esta condición de frontera con la definición original de A.C. cuya lattice es inicialmente infinita. 

Reglas de los Automatas

La regla establece el valor de una celda en función de sus 3 vecinos superiores. Esta regla es aplicada sobre la retícula varias veces dando como resultado configuraciones con distintas propiedades. Todos estos autómatas siempre empiezan con una serie de valores iniciales, y a partir de ahí, y aplicando las reglas, la retícula irá “creciendo”.

Las reglas se representas con un número binario de 8 dígitos, que representa la siguiente secuencia (las celdas negras representan 1s y las blancas 0s).

Si se fija uno atentamente en la fila de arriba de cada elemento representa los números del 0 al 7 en binario de derecha a izquierda (blanca-blanca-blanca = 000; blanca-blanca-negra = 001, ...), y el número de abajo representa cuál es el valor de la casilla de abajo dado sus tres vecinos superiores. Queda claro que, para todas las reglas de este tipo, un solo número binario de 8 cifras determinará el comportamiento de esta, ya que las casillas superiores siempre serán las mismas, y sólo cambiarán los resultados de abajo. Así, para la figura de arriba, el número binario que la representa es 00011110, que en decimal es 30. A esta regla se le conoce como la Regla 30.(fuente)

Ejemplos de Reglas

Regla 90

Esta regla también fue presentada por Stephen Wolfman en 1983 y se representa con el binario 01011010. A continuación mostramos su representación gráfica y una retícula tras pasar por 15 iteraciones.

Regla 184

La regla 184 viene representada por el binario 10111000, y a continuación mostramos su representación gráfica y un ejemplo de una retícula tras 16 iteraciones con esta regla.

Como se puede ver, este autómata aparentemente no ofrece nada usando la condición inicial que hemos estado usando en el resto de reglas. Veamos que resultado nos da con una condición de inicio aleatoria:

En base a lo anterior existe un algoritmo que, bien implementado, funciona con todas las reglas, el cual implementamos en el siguiente codigo:

Donde tenemos un metodo (generacionReglaBinario())que recibe el numero de la regla a aplicar para el automata y lo convierte a binario, facilitando la generación del mismo.Mientras tanto, el método (generacionHashMapRegla()) es el que genera el algoritmo para mostrar el patron correspondiente a la regla.

Ademas de crear la regla que el usuario elija, se da la opción de generar la primer generación de manera aleatoria o no. Al generarse de manera no aleatoria encendemos una celda a la mitad de la primer generación y a partir de ahí se empiezan a formar las generaciones nuevas. La generación aleatoria enciende celdas de la primer generación aleatoriamente para después crear las generaciones nuevas.

En el siguiente código se puede observar como es que se genera la primer generación no aleatoriamente.

En el código siguiente,podemos observar la manera en la que se genera aleatoriamente la primer generación.
La lógica para crear las siguientes generaciones fue crear un primer arreglo con la primer generación y a traves de búsquedas en el hashmap de la regla crear un arreglo con la siguiente generación para al final pasar esta ultima generación a el primer arreglo y asi sucesivamente.

El código completo puede encontrarse aqui

A continuación se muestra un video del programa funcionando.